THE NEW INTERPRETATION OF
PHOTOEFFECT
Ph.M. Kanarev
The Kuban State Agrarian
University, Department of Theoretical Mechanics
13, Kalinin Street, 350044
Krasnodar, Russia
E-mail: kanphil@mail.kuban.ru
Abstract: It has been disclosed that the equation
suggested by A. Einstein for the interpretation of photoeffect is a mathematical model of the law of formation of
the atom and ion spectra discovered in 1993.
Key words: energy, photon, electron, bond
INTRODUCTION
It is known that the most acceptable
interpretation of experimental dependencies of photoeffect has been suggested by A.
Einstein in 1905, and he got the Nobel prize for it [1], [2], [3]. He made it in the
absence of the law of formation of the atom and ion spectra. Now this law has been
discovered, and we can check correctness of its interpretation and the possibility of
deeper understanding of photoeffect [4], [5], [6], [7].
THEORETICAL PART
The mathematical model suggested by A.
Einstein for the interpretation of experimental dependencies of photoeffect has the
following form [3]
![]() ,
(1)
,
(1)
where ![]() is kinetic energy of the photoelectron emitted by
the photocathode;
is kinetic energy of the photoelectron emitted by
the photocathode; ![]() is energy of the photon, but it is not explained in
the papers, of which photon exactly [1], [2], [3],
is energy of the photon, but it is not explained in
the papers, of which photon exactly [1], [2], [3], ![]() is the
photoelectron exit work is a constant, which does not depend on frequency [1], [2], [3].
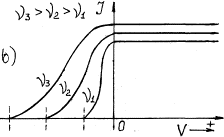
The main experimental dependencies of photeffect are given in Fig. 1 [2].
is the
photoelectron exit work is a constant, which does not depend on frequency [1], [2], [3].
The main experimental dependencies of photeffect are given in Fig. 1 [2].
|
|
Fig. 1. Dependence of photocurrent on
light intensity: a) at its constant frequency; b) at different frequency ![]()
Photocurrent takes place in the
photocathode-collector circuit. If the photocathode is exposed to monochromatic light (Fig. 1, a), the value of potential –![]() retarding the photoelectrons emitted by the photocathode
does not depend on light intensity. Light intensity increase increases photocurrent and
does not exert influence on the retarding potential value and, consequently, on kinetic
energy of the photoelectrons. If frequency of light, which strikes upon the photocathode,
is increased, the value of the negative potential –
retarding the photoelectrons emitted by the photocathode
does not depend on light intensity. Light intensity increase increases photocurrent and
does not exert influence on the retarding potential value and, consequently, on kinetic
energy of the photoelectrons. If frequency of light, which strikes upon the photocathode,
is increased, the value of the negative potential –![]() retarding
the photoelectrons is increased (Fig. 1, b).
retarding
the photoelectrons is increased (Fig. 1, b).
As the value of the retarding negative
potential –![]() is determined by kinetic
energy
is determined by kinetic
energy ![]() of the
electrons emitted by the photocathode under the influence of light illumination, it
results from the dependence shown in Fig. 1,b that kinetic energy
of the
electrons emitted by the photocathode under the influence of light illumination, it
results from the dependence shown in Fig. 1,b that kinetic energy ![]() of the photoelectrons emitted by them is increased
with the increase of frequency of the photons exposing the photocathode.
of the photoelectrons emitted by them is increased
with the increase of frequency of the photons exposing the photocathode.
Let us try to find a connection of Einstein’s equation (1)
with the mathematical model of the law of formation of the atom and ion spectra (2). We
have already shown that the mathematical model, which describes the spectra of the
multi-electron atoms and ions, has the following form [4], [10], [12]:
![]() ,
(2)
,
(2)
where ![]() is energy of the photon absorbed or emitted by the
electron;
is energy of the photon absorbed or emitted by the
electron; ![]() is ionization
energy of the electron; E1 is energy of the bond of the electron with the
atomic nucleus, which corresponds to its first energy level;
is ionization
energy of the electron; E1 is energy of the bond of the electron with the
atomic nucleus, which corresponds to its first energy level; ![]() is the main quantum number.
is the main quantum number.
The correlation (2) appears from
experimental spectroscopy, that’s why it is a mathematical model of the law of
formation of the atom and ion spectra. Einstein’s equation (1) describes similar
process of photon absorption by the electrons. It affords ground for supposition of
identity of the equations (1) and (2) and
uniformity of their interpretation. It appears from the given equations
![]() .
(3)
.
(3)
It means that if the electron loses bond
with the atomic nucleus, its kinetic energy ![]() is equal to energy
is equal to energy ![]() of the absorbed photon. Then
of the absorbed photon. Then
![]() .
(4)
.
(4)
It appears from this that ![]() energy value in
Einstein’s equation (1) is ionization energy
energy value in
Einstein’s equation (1) is ionization energy ![]() of the electron emitted by the photocathode
material. It appears from the equations (1) and (2) that
of the electron emitted by the photocathode
material. It appears from the equations (1) and (2) that
![]() .
(5)
.
(5)
The new clarification: photoelectron exit
work ![]() is equal to
binding energy of electron
is equal to
binding energy of electron ![]() when it is on a definite energy level in the atom
or the molecule.
when it is on a definite energy level in the atom
or the molecule.
Experimental investigations of
photoeffect are carried out usually with the photocathodes made of alkali metals [1]. For
example, it is known that the work of the photoelectron exit from the lithium photocathode
is equal to ![]() =2.4 eV [1]. Ionization energy of this electron is equal to
=2.4 eV [1]. Ionization energy of this electron is equal to ![]() =5.392 eV, and its binding energy with the nucleus
corresponding to the first energy level is equal to
=5.392 eV, and its binding energy with the nucleus
corresponding to the first energy level is equal to ![]() =14.05 eV
[4]. If we take it into account and use the mathematical model of the law of formation of
the atom and ion spectra (2), we’ll get a theoretical spectrum of this electron
=14.05 eV
[4]. If we take it into account and use the mathematical model of the law of formation of
the atom and ion spectra (2), we’ll get a theoretical spectrum of this electron ![]() (theor.), which
coincides completely with the experimental spectrum
(theor.), which
coincides completely with the experimental spectrum ![]() (exp.) (Table
1). Formula (5) gives an opportunity to calculate binding energies
(exp.) (Table
1). Formula (5) gives an opportunity to calculate binding energies ![]() of this electron with the atomic nucleus (according to Einstein, the exit work), which
correspond to all (
of this electron with the atomic nucleus (according to Einstein, the exit work), which
correspond to all (![]() ) energy levels of this
electron [4].
) energy levels of this
electron [4].
Table 1. Spectrum of the
first electron of the lithium atom
Volumes |
n |
2 |
3 |
4 |
5 |
6 |
|
eV |
- |
3.83 |
4.52 |
4.84 |
5.01 |
|
eV |
1.88 |
3.83 |
4.51 |
4.83 |
5.00 |
|
eV |
3.51 |
1.56 |
0.88 |
0.56 |
0.39 |
It is known that the like atoms are
united in a molecule with the covalent bond, and binding energies between valence
electrons correspond to fractional quantum numbers ![]() [4]. It allows us to determine what is a
photoelectron emission source: atoms or molecules of the photocathode material. If we
substitute
[4]. It allows us to determine what is a
photoelectron emission source: atoms or molecules of the photocathode material. If we
substitute ![]() =2.4 eV and
=2.4 eV and ![]() =14.05 eV in the formula
(5), we’ll find
=14.05 eV in the formula
(5), we’ll find ![]() =2.4. As value
=2.4. As value ![]() is a fractional
number, it means that the lithium molecules, not atoms are the source of the
photoelectrons (Table 1) [4].
is a fractional
number, it means that the lithium molecules, not atoms are the source of the
photoelectrons (Table 1) [4].
For a photoelectron of the sodium
photocathode, we have: ![]() =5.139 eV,
=5.139 eV, ![]() =13.086 eV and
=13.086 eV and ![]() =2.1 eV [1], [4]. If we
use the mathematical model of the law of formation of the atom and ion spectra (2),
we’ll get a sodium photoelectron spectrum (Table 2) [4].
=2.1 eV [1], [4]. If we
use the mathematical model of the law of formation of the atom and ion spectra (2),
we’ll get a sodium photoelectron spectrum (Table 2) [4].
Table 2. Spectrum of the 1st
electron of the sodium atom
Valumes |
n |
2 |
3 |
4 |
5 |
6 |
|
eV |
- |
3.68 |
4.31 |
4.62 |
4.78 |
|
eV |
- |
3.68 |
4.32 |
4.62 |
4.77 |
|
eV |
3.27 |
1.45 |
0.82 |
0.52 |
0.36 |
Value ![]() determined with the help of the formula (5) is
equal to
determined with the help of the formula (5) is
equal to ![]() =2.5. It appears from this that the sodium molecules, not
atoms are the source of the photoelectrons of the sodium photocathode.
=2.5. It appears from this that the sodium molecules, not
atoms are the source of the photoelectrons of the sodium photocathode.
The mathematical model of the law of formation of the atom and
ion spectra (2) shows that it has no orbital component of electron energy. It appears from
this that the electron has no orbital motion in the atom. The molecules are formed by
means of a combination of the unlike magnetic poles of their valence atomic electrons,
which are connected with the nuclear protons by means of the magnetic poles as well [4],
[8].
The analysis of the law of formation of
the atom and ion spectra (2) as well as the spectrum calculation results (Table 1 and 2)
show that binding energy ![]() of the electron with the atomic nucleus and,
consequently, binding energy of valence electrons of two atoms with each other is changed
step by step (5). It appears from this that kinetic energy of the photoelectrons
of the electron with the atomic nucleus and,
consequently, binding energy of valence electrons of two atoms with each other is changed
step by step (5). It appears from this that kinetic energy of the photoelectrons ![]() and value of
retarding potential –
and value of
retarding potential –![]() (Fig. 1, b) should be
changed step by step as well. The photoelectrons can absorb only the photons, which
correspond to their binding energies in the molecules of the given substance. The greater
binding energy between the electrons in the molecules, the greater photon energy is
required for the break of this bond and the greater kinetic energy the photoelectrons
being released will acquire, and the greater potential will be required for their
retardation on the way to the collector. Let us pay attention to the fact that the given
logical chain originates from the mathematical model of the law of formation of the atom
and ion spectra (2) and is present in Einstein’s equation implicitly (1).
(Fig. 1, b) should be
changed step by step as well. The photoelectrons can absorb only the photons, which
correspond to their binding energies in the molecules of the given substance. The greater
binding energy between the electrons in the molecules, the greater photon energy is
required for the break of this bond and the greater kinetic energy the photoelectrons
being released will acquire, and the greater potential will be required for their
retardation on the way to the collector. Let us pay attention to the fact that the given
logical chain originates from the mathematical model of the law of formation of the atom
and ion spectra (2) and is present in Einstein’s equation implicitly (1).
Current is present in the circuit due to
the fact that the photoelectrons emitted by the photocathode material molecules are
substituted by free electrons. They should emit the photons, which energy is equal to
binding energy of the electrons in the molecules, but light striking the photocathode does
not allow us to see this emission.
CONCLUSION
Mathematical Einstein’s equation
describing experimental regularities of photoeffect has deeper physical sense. When the
components of this equation are interpreted correctly, it becomes the mathematical model
of the law of formation of the atom and ion spectra discovered by us in 1993 and published
in the papers [9], [10], [11], [12], [4].
REFERENCES
1. Shpolsky E.V.. Atomic Physics. Volume 1. M.: 1963. 575 pages.
2.
R. Sprole. Modern Physics. Quantum Physics of Atoms of Solid Body and Nuclei. M.: Nauka,
1974. 591 pages
3.
Vikhman E.. Quantum Physics. M.: Nauka, 1977.
4. Kanarev Ph. M.. The Foundation of Physchemistry of Microworld. Krasnodar
2002. 320 pag. (In Russian and in English)
5.
Kanarev Ph. M.. Modelling the Photon and Analyzing Its
Electromagnetic and Physical Nature. Journal
of Theoretics. Vol. 4 – 1. http://www.journaloftheoretics.com
6. Kanarev Ph.M.
Model for the Free Electron. Galilean Electrodynamics. Volumes 13, Special Issues 1. Spring 2002. pag. 15-18.
7. Kanarev
Ph.M. Model of the Electron. «Apeiron» V.
7, no. 3-4, 2000. Pag. 184-193. http://redshift.vif.com
8. Kanarev Ph.M.
Electrons in Atoms. Journal of
Theoretics. Vol. 4 –4. http://www.journaloftheoretics.com
9.
Kanarev Ph.M.. Analysis of Fundamental Problems of Modern Physics. Krasnodar. 1993. 255
pages.
10. Kanarev Ph.
M.. The Analytical Theory of Spectroscopy.
Krasnodar, 1993. 88 pag. (In English).
11. Kanarev Ph.M. On The Way to The Physics of The XXI Century. Krasnodar.
1995. Pag. 269. (In English).
12.
Kanarev Ph.M.. Law of Formation of the Spectra of the Atoms and Ions. Proceedings of the
international conference “Problems of space, time, gravitation”. St.-Petersburg.
Publishing house “Polytechnic”, 1997, pp. 30-37.