THE DOPPLER EFFECT AT PHOTON EMISSION
Ph.M. Kanarev
The Kuban State Agrarian University, Department of
Theoretical Mechanics
13, Kalinin St., 350044 Krasnodar,
Russia
E-mail: kanphil@mail.kuban.ru
Abstract: It is shown that the Doppler Effect calculation
at photon emission is possible only with the help of classical mathematical models.
Key
words: The Lorentz transformations, the
Doppler Effect, infrared and ultraviolet shift of the spectra, velocity of light, velocity of source.
Introduction
The results of our investigations confirm Albert Einstein’s correctness in his
dispute with Niels Bohr [1], [2], [3]. Einstein’s answer to the venerators of his
talent has proved to be a prophetic one: “It seems to them that I look at the results
of my life with a halcyon satisfaction. But everything is to the contrary if examined
closely. There exists no concept, in relation to which I am sure that it will remain
inviolable, and I am not convinced that I am on the right track.” (F. Gernek. Albert
Einstein. M., 1966, page 16) [4]. The following facts confirm equity of these words.
There are two interpretations of this effect: the
relativistic interpretation and the classical one [3], [5], [6], [7].
The
Relativistic Interpretation of the Doppler Effect
The relativistic interpretation is based on the second Einstein’s postulate
[8]: Any ray of light moves
in the stationary system of co-ordinates with the determined velocity, whether the ray be
emitted by a stationary or a moving body. The Lorentz transformations originate from this wording
of the postulate (Fig. 1) [2], [3]:
![]() ;
(1)
;
(1)
![]() ,
(2)
,
(2)
where: ![]() and
and ![]() are spatial intervals measured in moving
are spatial intervals measured in moving ![]() and stationary
and stationary ![]() reference
systems, respectively (Fig. 1);
reference
systems, respectively (Fig. 1); ![]() and
and ![]() is time measured in moving and stationary reference systems, respectively;
is time measured in moving and stationary reference systems, respectively; ![]() is traverse
speed of moving reference system;
is traverse
speed of moving reference system; ![]() is velocity of
light.
is velocity of
light.
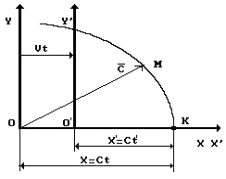
Fig. 1. Diagram to analysis of the Lorentz transformations
[2], [3]
It is clear from Fig. 1 that ![]() and
and ![]() . If we insert these
values in the formula (1) or (2), we’ll find
. If we insert these
values in the formula (1) or (2), we’ll find
![]() (3)
(3)
or
![]() ,
(4)
,
(4)
where ![]() and
and ![]() are frequencies of electromagnetic emission in the
moving and stationary reference systems, respectively.
are frequencies of electromagnetic emission in the
moving and stationary reference systems, respectively.
If we designate ![]() ,
we’ll have
,
we’ll have
![]() (5)
(5)
This is the relativistic mathematical model of the calculation of the Doppler
Effect [3], [8]. As ![]() ,
it results from the ratios (4) and (5) that emission frequency
,
it results from the ratios (4) and (5) that emission frequency ![]() of the moving source is greater than radiation
frequency
of the moving source is greater than radiation
frequency ![]() of stationary
source, i.e. the mathematical models (4) and (5) describe only ultraviolet shift of the
spectra. Let us pay attention to the fact that in the ratios (4) and (5) the directions of
velocities of source
of stationary
source, i.e. the mathematical models (4) and (5) describe only ultraviolet shift of the
spectra. Let us pay attention to the fact that in the ratios (4) and (5) the directions of
velocities of source ![]() and the emitted photon
and the emitted photon ![]() coincide with the directions of axes
coincide with the directions of axes ![]() and
and ![]() .
.
If we write the ratio (5) in the following form
![]() ,
(6)
,
(6)
it will show to what extent frequency ![]() of the photon emitted from the stationary source
(Fig. 1) is less than frequency
of the photon emitted from the stationary source
(Fig. 1) is less than frequency ![]() of the photon
emitted by the moving source, and it will not characterize the infrared shift of the
spectra. As in both formulas (5) and (6)
of the photon
emitted by the moving source, and it will not characterize the infrared shift of the
spectra. As in both formulas (5) and (6) ![]() , both formulas describe
the ultraviolet shift of the spectra, and we have no right to use the mathematical model
(6) for the calculation of the infrared shift of the spectra [3].
, both formulas describe
the ultraviolet shift of the spectra, and we have no right to use the mathematical model
(6) for the calculation of the infrared shift of the spectra [3].
Let us prescribe several values ![]() and determine values
and determine values ![]() (5) and
(5) and
![]() (6)
for them (Table 1).
(6)
for them (Table 1).
Table
1
Relativistic
results of calculation of the Doppler Effect
|
|
|
0.000001 0.00001 0.0001 0.001 0.01 0.1 |
1.0000009 1.0000099 1.0000999 1.0010004 1.0100504 1.1055415 |
0.9999989 0.9999899 0.9998999 0.9990004 0.9900494 0.9045340 |
The results of Table 1 show
unambiguously that frequency ![]() of the emitted photon is increased with the
increase of velocity
of the emitted photon is increased with the
increase of velocity ![]() of movement of the reference system (for example,
of a star). It means that an ultraviolet shift of the spectral lines is increased.
Physical sense being present in mathematical symbols
of movement of the reference system (for example,
of a star). It means that an ultraviolet shift of the spectral lines is increased.
Physical sense being present in mathematical symbols ![]() and
and ![]() deprives us of the right to give another
interpretation of the mathematical models (5) and (6).
deprives us of the right to give another
interpretation of the mathematical models (5) and (6).
Thus, we have got an unambiguous answer: the relativistic mathematical models (5)
and (6) describe only ultraviolet shift of the spectra, and they are not connected with
their infrared shift [5].
In science, the Lorentz transformations (1) and (2) have been used for the
calculation of the so called relativistic effects for about a hundred years. Now we get to
know that they give the possibility to calculate the relativistic effects only for the
ultraviolet shift of the spectra and provide no information concerning the relativistic
effects by the infrared shift of the spectra. It means that the Lorentz transformations
misrepresent the reality. Now we can check this fact using the axiom of space-matter-time unity [2], [3].
Let us pay attention to the fact that formula (1) has coordinate ![]() , which is fixed in the moving reference system (Fig. 1),
and formula (2) has time
, which is fixed in the moving reference system (Fig. 1),
and formula (2) has time ![]() , which flows in the same
reference system. Thus, in mathematical formulas (1) and (2) an oscillating quantity of
the spatial interval
, which flows in the same
reference system. Thus, in mathematical formulas (1) and (2) an oscillating quantity of
the spatial interval ![]() in the moving reference system is separated from
time
in the moving reference system is separated from
time ![]() , which flows in this reference system. As in reality it is
impossible to separate space from time, it is impossible to analyze these equations
separately. This is a set of equations, and it is necessary to analyze them together. This
analysis alone will correspond to the axiom of space-matter-time unity, and the results of such
analysis alone will reflect reality.
, which flows in this reference system. As in reality it is
impossible to separate space from time, it is impossible to analyze these equations
separately. This is a set of equations, and it is necessary to analyze them together. This
analysis alone will correspond to the axiom of space-matter-time unity, and the results of such
analysis alone will reflect reality.
It results from equation (1) implicitly that by ![]() the spatial interval value
the spatial interval value ![]() is reduced. Thereof modern physicists make a
conclusion that the spatial interval value
is reduced. Thereof modern physicists make a
conclusion that the spatial interval value ![]() is reduced with the increase of velocity
is reduced with the increase of velocity ![]() of movement of
the moving reference system. Then, they take one equation (2) for the analysis[1].
It appears from this implicitly that by
of movement of
the moving reference system. Then, they take one equation (2) for the analysis[1].
It appears from this implicitly that by ![]() the spatial interval value
the spatial interval value ![]() is reduced. Thereof they make a conclusion that if
traverse velocity of the moving reference system is increased, flow rate of time
is reduced. Thereof they make a conclusion that if
traverse velocity of the moving reference system is increased, flow rate of time ![]() in it is
reduced.
in it is
reduced.
Let us correct erroneous interpretation. As in reality it is impossible to separate
space from time, let us analyze equations (1) and (2) together; for this purpose, let us
divide the fist one by the second one; as a result, we’ll have
![]() (7)
(7)
Now mathematical formula (7) reflects dependence of coordinate ![]() on time
on time ![]() . It appears from this
that formula (7) operates within the framework of the axiom of space-matter-time unity, i.e. within the
framework of reality.
. It appears from this
that formula (7) operates within the framework of the axiom of space-matter-time unity, i.e. within the
framework of reality.
It
is clear from Fig. 1 that ![]() is the coordinate of position of a light signal in
the stationary reference system. If we insert
is the coordinate of position of a light signal in
the stationary reference system. If we insert ![]() in the given formula (7), we’ll get
coordinate
in the given formula (7), we’ll get
coordinate ![]() , which positions the light signal in the moving reference
system. Where is this signal situated? As we change coordinates
, which positions the light signal in the moving reference
system. Where is this signal situated? As we change coordinates ![]() and
and ![]() , in time
, in time ![]() and
and ![]() it is situated
on coinciding axes
it is situated
on coinciding axes ![]() and
and ![]() , i.e. in point
, i.e. in point
![]() (Fig. 1).
Geometrical sense of the Lorentz
transformations is very simple. Coordinate
(Fig. 1).
Geometrical sense of the Lorentz
transformations is very simple. Coordinate ![]() of point
of point ![]() in the moving reference system and its coordinate
in the moving reference system and its coordinate ![]() in the
stationary reference system are positioned in them. It is a crossing point of a light
sphere with axes
in the
stationary reference system are positioned in them. It is a crossing point of a light
sphere with axes ![]() and
and ![]() (Fig. 1). This is the essence of the Lorentz
transformations. There is no other information in these transformations, and they reflect
no physical effects [2], [3].
(Fig. 1). This is the essence of the Lorentz
transformations. There is no other information in these transformations, and they reflect
no physical effects [2], [3].
Classical Interpretation of the Doppler Effect at Photon Emission
We
have already shown that total energy of the photon is equal to the sum of energies of its
translational motion ![]() and
rotational motion
and
rotational motion ![]() and that this
amount depends on the value of speed
and that this
amount depends on the value of speed ![]() and
direction of radiation source motion
and
direction of radiation source motion ![]() [1],
[2], [3]. If the angle between the direction of velocity vector of source motion
[1],
[2], [3]. If the angle between the direction of velocity vector of source motion ![]() and the direction of velocity vector of the photon
being emitted (Fig.2) is equal
and the direction of velocity vector of the photon
being emitted (Fig.2) is equal ![]() ,
total energy of the emitted photon will be written in the following way [7].
,
total energy of the emitted photon will be written in the following way [7].
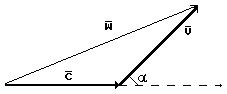
Fig. 2. Diagram of addition of velocities of the source
and the photon
![]() (8)
(8)
If we take into
account that ![]() and designate
and designate
![]() , we’ll
find after conversion of the equation (8)
, we’ll
find after conversion of the equation (8)
![]() (9)
(9)
If the directions
of the motion of the source and the photon being emitted coincide, it means that ![]() and
and
![]() (10)
(10)
When
the directions of the motion of the source and the photon being emitted are counter, it
means that ![]() and
and
![]() (11)
(11)
In
Table 2, the calculation results are given according to the classical formulas (10) and
(11) and relativistic formulas (5) and (6). Analysis of this table shows that the
classical formula (10) gives the result, which is close to the result of the relativistic
formula (5), and classical formula (11) gives the result, for which there is no
relativistic formula,
Relativists use
the formula (6) for the calculation of the infrared shift of the spectra having no
mathematical right for it. Such right and such accuracy are given by the classical
mathematical formula (11) (Table 2).
Table 2
Calculation results of Doppler Effect
|
|
|
|
|
0.000001 0.00001 0.0001 0.001 0.01 0.1 |
1.0000010 1.0000100 1.0001000 1.0010005 1.0100500 1.1050000 |
0.9999990 0.9999900 0.9999000 0.9990005 0.9900500 0.9050000 |
1.0000009 1.0000099 1.0000999 1.0010004 1.0100504 1.1055415 |
0.9999989 0.9999899 0.9998999 0.9990004 0.9900494 0.9045340 |
The results of the simultaneous registration of the usual spectral lines of the
hydrogen atom received from the space object SS433 and the spectral lines shifted to the
ultraviolet and infrared field of the spectrum can serve as an experimental fact, which
confirms equity of mathematical models (10) and (11) [9]. It proves the fact that the main
part of the space object SS433 is stationary in relation to space, and two other parts
move in relation to space. The part, which generates the ultraviolet shift, moves to the
Earth, and the part, which generates the infrared shift at that time, moves from the
Earth. Periodicity of the change of values of these shifts is registered [9].
CONCLUSION
The relativistic mathematical model (6), which originates from the Lorentz
transformations, has nothing to do with the Doppler Effect.
The ultraviolet and infrared shifts of the spectra describe the classical
mathematical models (10) and (11) only.
REFERENCES
1. Kanarev Ph. M. Modelling the Photon and
Analyzing Its Electromagnetic and Physical Nature. Journal of Theoretics. Vol. 4-1, February 2002.
2. Kanarev
Ph. M. On the Way to the Physics of the XXI Century, Krasnodar, 1995, 269 pages (in
English).
3. Kanarev Ph. M.
The Foundations of Physchemistry of Microworld. Krasnodar. 2002. 320 pages (in Rusian
and in English).
4. Hernek F. Albert Einstein. Life for Truth, Humanism and Peace. M.: Progress. 1966.
5. Macarthur D.W., Butterfield
K.B., Clark D.A., Donahue J.B. and Gram P.A.M., Brgant H.C., Smith W.W. and Comtet G. Test of the
Special Relativistic Doppler Formula at ![]() . Physical Review
Letters. Vol. 56, no. 4, pp. 282-285. 1986.
. Physical Review
Letters. Vol. 56, no. 4, pp. 282-285. 1986.
6. Pobedonostsev
L. A. Experimental investigation of the Dopler effect. Galilean Electrodynamics.
Vol. 3, no. 2, pp. 33-35. (March/April 1992).
7. L. B. Boldyreva, N.B. Sotina. The Possibility of Developing a Theory of Light Without Special Relativity. “Galilean Electrodynamics” . Volume13, Number 6. Pag. 103-107.
8. Einstein A. To electrodynamics of moving bodies.
Collection of articles on special theory of relativity. M. Atomizdat.
1973.
9. Chernin A.D. Stars and
Physics. M. Nauka, 1984. 160 pages.