<<
Back to Kanarev's Physchemistry Book Index
10. MODELS OF THE ATOMS AND THE MOLECULES
10.1. General
The mathematical model of the law of formation of the
spectra of the atoms and the ions (207) proves the lack of orbital motion of
the electrons in the atoms. The atomic nucleus models built by us confirm this
fact.
The protons in the
atomic nuclei are arranged on their surface and have a free magnetic pole for
the connection with the like magnetic pole of the electron. The chain of
consistency of actions of Nature determined in this search confirms adjacency
of the models of the electron, the proton and neutron to reality. That’s why we
can get ahead and begin to analyze the structure of the atoms of chemical
elements. The hydrogen atom is the first and the simplest atom. Let us check
the ideas described by us taking its formation as an example.
10.2. Structure of
the Hydrogen Atom
The largest array
of experimental information concerning the hydrogen atom is in its spectra [5],
[25]. In order to determine the structure of the hydrogen atom, we should
analyze this information. We have already given the calculation of the spectrum
of the hydrogen atom. As the hydrogen atom model is built on the basis of this
calculation, let us give this calculation one again. First of all. Let us calculate
the energies ![]() of the photons
radiated and absorbed by the electron during its transitions and the binding
energies
of the photons
radiated and absorbed by the electron during its transitions and the binding
energies ![]() of the electron with
the atomic nucleus (proton), which correspond to these transitions.
of the electron with
the atomic nucleus (proton), which correspond to these transitions.
In order to
calculate the energies ![]() of the photons
absorbed or radiated by the electron during its transitions, we’ll use the
spectrum formation law discovered by us
(207) [33], [53], [109] and the experimental spectroscopy data [5],
[25].
of the photons
absorbed or radiated by the electron during its transitions, we’ll use the
spectrum formation law discovered by us
(207) [33], [53], [109] and the experimental spectroscopy data [5],
[25].
We’ll calculate
binding energy ![]() of the electron with
the nucleus, which corresponds to any energy level, according to the formula
(206).
of the electron with
the nucleus, which corresponds to any energy level, according to the formula
(206).
Taking into
consideration the fact that ionization energy ![]() of the hydrogen atom
is equal to binding energy
of the hydrogen atom
is equal to binding energy ![]() of the electron with
the nucleus, which corresponds to the first energy level
of the electron with
the nucleus, which corresponds to the first energy level ![]() and using the
formulas (212) and (213), we’ll get the energies of the photons
and using the
formulas (212) and (213), we’ll get the energies of the photons ![]() (theor.) radiated or absorbed by the electron and binding
energies
(theor.) radiated or absorbed by the electron and binding
energies ![]() (theor.) of the
electron with the atomic nucleus, which correspond to n-energy levels (Table
27).
(theor.) of the
electron with the atomic nucleus, which correspond to n-energy levels (Table
27).
Table 27. Spectrum
of the hydrogen atom
|
Values |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
10.20 |
12.09 |
12.75 |
13.05 |
13.22 |
|
|
eV |
10.198 |
12.087 |
12.748 |
13.054 |
13.22 |
|
|
eV |
3.40 |
1.51 |
0.85 |
0.54 |
0.38 |
It follows from the
spectroscopy law (212) that the energies of absorbed and radiated photons
during the transition of the electron between the energy levels n and n+1 are
calculated according to the formula (216).
Let us list the
results of the calculation (Table 6) of the energies of the photons ![]() (theor.) radiated or
absorbed by the electron of the hydrogen atom during transitions between the
levels n and n+1 as compared with the experimental
(theor.) radiated or
absorbed by the electron of the hydrogen atom during transitions between the
levels n and n+1 as compared with the experimental ![]() (exper.) data.
(exper.) data.
Table 28. Energies
of interlevel transitions of the electron of the hydrogen atom
|
Levels |
n, n+1 |
2...3 |
3...4 |
4...5 |
5...6 |
6...7 |
7...8 |
|
|
eV |
1.89 |
0.66 |
0.30 |
0.17 |
0.10 |
0.07 |
|
|
eV |
1.88 |
0.661 |
0.306 |
0.166 |
0.100 |
0.065 |
We should note that
binding energies ![]() of the electron with
the atomic nucleus are specified in Table 27. Other energies of the radiated or
absorbed photons during the transitions of the electron are given in Table 28.
of the electron with
the atomic nucleus are specified in Table 27. Other energies of the radiated or
absorbed photons during the transitions of the electron are given in Table 28.
The formula (216)
gives the possibility to calculate the energies of the radiated and absorbed
photons during any transitions of the electron. For example, when the electron
goes from the 1st to the 10th energy level, it absorbs the photon with the
energy, which is calculated according to the formula
![]() (236)
(236)
If the electron
goes from, say, the 15th to the 10th energy level, it radiates the photon with
energy
![]() (237)
(237)
Let us see how free
electron energy will be changed during absorption and emission of the photons.
As ionization energy of the hydrogen atom is equal to ![]() =13.598 eV, it means that when the free electron is united
with the nucleus of the hydrogen atom (the proton)
=13.598 eV, it means that when the free electron is united
with the nucleus of the hydrogen atom (the proton) ![]() , it should emit the photon with the energy being equal to
ionization energy and occupy the first
(n=1) non-exited energy level. Its full energy 511.100 eV is reduced and
becomes equal to
, it should emit the photon with the energy being equal to
ionization energy and occupy the first
(n=1) non-exited energy level. Its full energy 511.100 eV is reduced and
becomes equal to
![]() (238)
(238)
Then,
after absorption of the photon with energy of 10.20 eV and the transfer to the
second energy level the complete energy of the electron will be increased and
will become
![]() (239)
(239)
Thus, during the
transitions to higher energy levels the electron increasing its full energy due
to the absorbed photons approximates its value to the energy value, which it
has in free state. This increase takes place at the expense of the absorbed
photons, and binding energy ![]() of the electron with
the proton being decreased approximates to zero (Table 27), and it becomes
free. All electrons of any atom act in such a way, and its allows them to be in
free state with one and the same mass and with one and the same charge. That’s
why mass and charge of all free electrons are always constant.
of the electron with
the proton being decreased approximates to zero (Table 27), and it becomes
free. All electrons of any atom act in such a way, and its allows them to be in
free state with one and the same mass and with one and the same charge. That’s
why mass and charge of all free electrons are always constant.
Thus, we have
agreed that free electron energy is equal to its photon energy ![]() . It means that in order to calculate radius
. It means that in order to calculate radius ![]() of the electron when
it is on the first energy level in the hydrogen atom, it is necessary to take
free electron energy and to subtract the energy, which it has radiated in the
form of the photon, from it. During the determination of the electron radius
when it is at the first energy level, this energy is equal to
522100-13.6=511086.4 eV. The value of the electron radius will be as follows
of the electron when
it is on the first energy level in the hydrogen atom, it is necessary to take
free electron energy and to subtract the energy, which it has radiated in the
form of the photon, from it. During the determination of the electron radius
when it is at the first energy level, this energy is equal to
522100-13.6=511086.4 eV. The value of the electron radius will be as follows
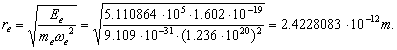
(240)
This value differs
from the value, which is calculated taking into consideration full energy of
the electron (138) for nominal value of ![]() .
.
It is clear that
the energy and, consequently, the electron radius in the atom are changed
insufficiently, and this fact matches the constant value of Compton wavelength
of the electron, which now we should call Compton radius of the electron.
We have already
shown that photon mass ![]() , radius
, radius ![]() and frequency
and frequency ![]() are changed in such a
way that their product (
are changed in such a
way that their product (![]() ) remains constant, because the change of a set of the
above-mentioned parameters is governed by the law of conservation of angular
momentum [11], [40]. The same law governs a change of the same set of the
parameters of the electron.
) remains constant, because the change of a set of the
above-mentioned parameters is governed by the law of conservation of angular
momentum [11], [40]. The same law governs a change of the same set of the
parameters of the electron.
Let us pay
attention to one more important fact. Binding energy of the electron with the nucleus
is changed in proportion to the change of square of frequency ![]() [70]. But if we
consider the dependence of frequency
[70]. But if we
consider the dependence of frequency ![]() of electron rotation
relative to its axis of symmetry from strength
of electron rotation
relative to its axis of symmetry from strength ![]() of magnetic field of
the electron (148), one more reason of the change of electron bond energy with
the nucleus takes place during its energy transition [70]
of magnetic field of
the electron (148), one more reason of the change of electron bond energy with
the nucleus takes place during its energy transition [70]
![]() (241)
(241)
As angular
rotational speed of the electron is proportional to its magnetic field
strength, we substitute strength ![]() of its magnetic field
for electron rotational speed
of its magnetic field
for electron rotational speed ![]() in the mathematical expression,
which determines electron energy,
in the mathematical expression,
which determines electron energy,
![]()
![]() (242)
(242)
and get the same
result, but with another physical meaning: electron energy is aliquot not to
angular frequency ![]() , but to strength
, but to strength ![]() of magnetic field of
the electron. It is an important consequence. It points out to possible
lack of rotation of the electron in relation to its axis in the moment when it is in the atom.
of magnetic field of
the electron. It is an important consequence. It points out to possible
lack of rotation of the electron in relation to its axis in the moment when it is in the atom.
We’d like to draw
our readers’ attention to the result of the joint solution of the relations
(14), (18), (148), (150) and (241)
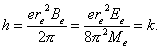 (243)
(243)
Is it a new
constant?
Hydrogen is the
simplest atom. It has one electron, and its nucleus consists of one proton. The
information found out by us concerning the structure of the electron and proton
gives the opportunity to get a notion about the formation process of this atom
[94].
One can suppose
that magnetic fields of both the proton and the electron are similar to
magnetic fields of the bar magnets and have magnetic poles. As proton mass is
much more greater than electron mass, the hydrogen mass formation will begin
with the convergence of the electron to the proton. We know that in free sate
the electron has magnetic moment and rather large magnetic field strength in
its geometrical centre, that’s why both electrical force and magnetic forces
will govern the process of the convergence of the electron with the proton at
the first stage.
As the magnetic
fields of both the proton and the electron have the largest strength about
their axes of rotation, the electron and the proton will rotate align during
the convergence. If their opposite magnetic poles are directed to meet each
other, both the electrical forces and the magnetic ones will draw the electron
and the proton together, and the proton will absorb the electron and will
become a neutron. As the results obtained
by the Japanese investigators have shown [51], this process is realized during
plasma electrolysis of water. When the electron is drawn together with
the proton and their like magnetic poles are directed to meet each other,
Coulomb’s forces acting not along the convergence axis, but normally to
toroidal surface of the electron will draw it together with the proton, and magnetic
forces will repulse them from each other. An equilibrium will be set between
these forces, and the structure being formed is such a way is the hydrogen atom
(Fig. 50). This phenomenon is confirmed by the results of the investigations of
plasma electrolysis of water [70].
A question arises:
how does the electron move in relation to the atomic nucleus if it has no
orbital movement? As the law (88, 214, 215) reflects the electron rotation only
in relation to its axis, the electron with the nucleus can interact only by the
axis of rotation. It can be presented in the form of a rotating peg-top, which
electromagnetic axis of rotation rests on the atomic nucleus, and it rotates in
relation to its axis of symmetry (Fig. 50).
The nature has made
the electron in such a way that it has electric field, which form is similar to
a spherical one and magnetic field is similar to magnetic field of the bar
magnet. The forces of unlike electrical fields bring the electron close to the
atomic nucleus, and the forces of their like magnetic poles limit this
approximation.
Thus, it appears
from the results of our investigations that the atomic nucleus has the size by
a factor of ![]() less than the size of
the electron. It is arranged on its axis, at a certain distance
less than the size of
the electron. It is arranged on its axis, at a certain distance ![]() from the geometrical
centre of the electron, which can be calculated taking Coulomb’s law as the
base. It gives the opportunity to determine the distance between the proton and
the electron when it is on the first energy level. As the binding energy of the
proton with the electron is equal to
from the geometrical
centre of the electron, which can be calculated taking Coulomb’s law as the
base. It gives the opportunity to determine the distance between the proton and
the electron when it is on the first energy level. As the binding energy of the
proton with the electron is equal to ![]() in this case, we’ll
have the following expression when
in this case, we’ll
have the following expression when ![]() .
.
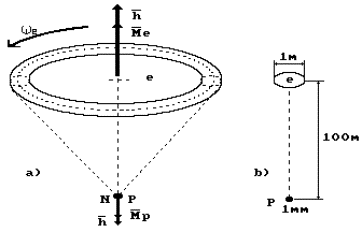
Fig. 50. Diagram of
the hydrogen atom model
![]() (244)
(244)
The calculation
results ![]() for n=2,3,4…. are
given in Table 29.
for n=2,3,4…. are
given in Table 29.
Table 29. Spectrum
of the hydrogen atom, its binding energy ![]() between the proton
and the electron and distances
between the proton
and the electron and distances ![]() between them
between them
|
Volumes |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
10.20 |
12.09 |
12.75 |
13.05 |
13.22 |
|
|
eV |
10.198 |
12.087 |
12.748 |
13.05 |
13.22 |
|
|
eV |
3.40 |
1.51 |
0.85 |
0.54 |
0.38 |
|
|
|
4.23 |
9.54 |
16.94 |
26.67 |
37.89 |
Minimal distance,
at which the electron comes to the proton, is ![]() (234), i.e. of the
order of Angstrom; it agrees with the hydrogen atom size accepted in modern
physics (Fig. 50).
(234), i.e. of the
order of Angstrom; it agrees with the hydrogen atom size accepted in modern
physics (Fig. 50).
If we accept that
the size of the proton is equal to one millimeter, the size of the electron
will be nearly one meter, and the distance between the nucleus of the hydrogen
atom (the proton) and the electron will be equal to one hundred meters (Fig.
50, b).
In Fig. 51, a
diagram of the consecutive transition of the electron of the hydrogen atom from
the first energy level (I) to the second one (II), from the second one to the
third one (III) and from the third one to the fourth one (IV) is shown.
As it is clear,
binding energy of the electron with the proton P at the moment of its stay at
the first (I) energy level is equal to ![]() =13.6 eV, and full energy is
=13.6 eV, and full energy is ![]() =5.11×105 eV.
After absorption of the photon with energy
=5.11×105 eV.
After absorption of the photon with energy
![]() =10.2 eV, the electron goes to the second (II) energy level,
and its binding energy becomes equal to
=10.2 eV, the electron goes to the second (II) energy level,
and its binding energy becomes equal to
![]() =3.4 eV. When the photon with energy
=3.4 eV. When the photon with energy ![]() =1.89 eV is absorbed, the electron goes to the third (III)
energy level, and its binding energy with the nucleus becomes equal to
=1.89 eV is absorbed, the electron goes to the third (III)
energy level, and its binding energy with the nucleus becomes equal to ![]() =1.51 eV, etc.
=1.51 eV, etc.

Fig. 51. Diagram of
addition of vectors of energies of the photon ![]() , the electron
, the electron ![]() and binding energy of
the electron with the atomic nucleus
and binding energy of
the electron with the atomic nucleus ![]() … in the absorption processes; I, II, III… are energy levels
of the electron
… in the absorption processes; I, II, III… are energy levels
of the electron
When binding energy
![]() wit the electron with
the nucleus is increased, it comes nearer to the atomic nucleus or is submerged
deeper into its cell. We understand ‘the cell” as a volume of a conical form
with the apex at the atomic nucleus, in which the electron rotates like the
peg-top. The larger the binding energy of the electron with the nucleus, the
nearer it is situated to the nucleus or the deeper in its cell.
wit the electron with
the nucleus is increased, it comes nearer to the atomic nucleus or is submerged
deeper into its cell. We understand ‘the cell” as a volume of a conical form
with the apex at the atomic nucleus, in which the electron rotates like the
peg-top. The larger the binding energy of the electron with the nucleus, the
nearer it is situated to the nucleus or the deeper in its cell.
When the photons
are absorbed, binding energy of the electron with the nucleus is reduced, and
it goes on rotating and precessing on the nucleus and with draws from it coming nearer to the surface of the
atom. When the electron emits the photons, its binding energy with the atomic nucleus
is increased, and it is submerged deeper in its “cells”.
It is important that there are no trigonometric functions in the mathematical
expression (212) of the spectrum formation law. It means that the processes of
absorption and emission of the photons by the electrons take place only in case
when vectors of their single energies are directed along one straight line. If
it were not the case, the correction factors or trigonometric functions would
be present in the spectrum formation law of the atoms and ions. But we cannot
exclude the possibility of emergence of these factors and trigonometric
functions during the calculation of the spectra of the atoms with many
electrons and the ions.
Thus, the hydrogen atom is a core with the positively
charge proton at one end and the negatively charged electron at the second end.
The size of the electron is by a factor of ![]() less than the size of
the atom itself, and the size of the proton is by a factor of
less than the size of
the atom itself, and the size of the proton is by a factor of ![]() less than the size of
the electron and by a factor of
less than the size of
the electron and by a factor of ![]() less than the size of
the atom (Fig. 50, b).
less than the size of
the atom (Fig. 50, b).
As magnetic moment
of the electron (![]() ) is by a factor of
) is by a factor of ![]() greater than the
magnetic moment of the proton (
greater than the
magnetic moment of the proton (![]() ) and as their vectors in the hydrogen atom are directed in
the opposed ways, magnetic moment of the hydrogen atom is practically equal to
magnetic moment of the electron or Bohr magneton`
) and as their vectors in the hydrogen atom are directed in
the opposed ways, magnetic moment of the hydrogen atom is practically equal to
magnetic moment of the electron or Bohr magneton`![]()
![]() (245)
(245)
Besides, equality
of spins of the electron and the proton and their opposite directivity make the
hydrogen atom spin equal to zero.
The hydrogen atom
model shown in Fig. 50 demonstrates its activity. On the one hand, there is a
positively charged proton, which is ready to be connected with a free electron;
on the other hand, there is a negatively charged electron, which is ready to be
connected with a proton or an electron. That’s why the hydrogen atoms can exist
only at high temperature (5000…10000)![]() C. At this temperature the atomic electrons are in exited
state, i.e. at the highest energy levels where their bond with the protons is
very weak.
C. At this temperature the atomic electrons are in exited
state, i.e. at the highest energy levels where their bond with the protons is
very weak.
The cause of the
emission of the photons during approximation of the electron with the proton
can be described in the following way. During the coaxial approximation of the
electron with the proton different numbers of their revolution in relation to
one and the same axis form the moment of forces, which will inhibit or
accelerate rotation of the electron. In the initial stage, the moments of
forces of the proton and the electron will be different. In order to restore
equality of these moments, the electron emits a part of its mass in the form of
the photon or absorbs it from the environment and is brought nearer or comes
off from the proton.
Here one should
take into account the photon condition of the environment. If the concentration
of the photons, which are necessary for the electron for the transition to the
next energy level, is enough, it will absorb such photon and make the
corresponding energy transition. If there is a lack of the photons, which
correspond to the existence of the electron at the definite energy level, in
the environment, it will emit this photon and will move to lower energy level.
The necessary equilibrium of the photons is preserved in the environment, which
determines its temperature. It is necessary to analyze photon pressure on
everything that exists in the photon environment in the same way as, for example,
in liquid or gaseous medium, but we’ll not consider this necessity, because
there exist more interesting tasks.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index